Discover the World of Pancyclic and Bipancyclic Graphs: A Gateway to Mathematical Marvels

Welcome to the exciting realm of Pancyclic and Bipancyclic Graphs! In this article, we will dive deep into the fascinating world of graph theory and explore the profound concepts behind these mathematical marvels. Prepare to be amazed as we unravel the secrets hidden within these seemingly simple structures.

What are Pancyclic and Bipancyclic Graphs?

Before we embark on this captivating journey, let's quickly grasp the fundamentals. In graph theory, a graph consists of vertices (also called nodes) connected by edges. Pancyclic and Bipancyclic Graphs fall under the category of special graph classes with intriguing properties.

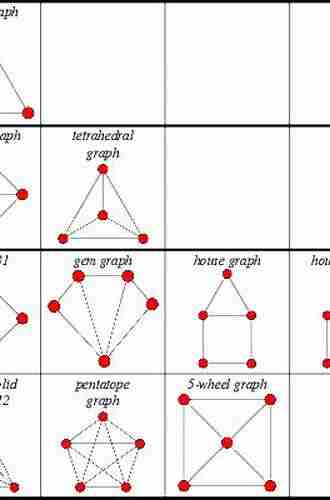
A pancyclic graph is a graph that contains cycles of every possible length. Simply put, it can be traversed in a cyclic manner, where the length of the cycle can vary. Imagine a graph that allows you to traverse through its vertices, following different paths of varying lengths, never missing any vertex. That's the essence of a pancyclic graph!

Pancyclic and Bipancyclic Graphs (SpringerBriefs in Mathematics)

by William Kercher(1st ed. 2016 Edition, Kindle Edition)

4.6 out of 5

Language	:	English
File size	:	3640 KB
Print length	:	120 pages
Screen Reader	:	Supported

FREE

On the other hand, a bipancyclic graph is a more specific type of pancyclic graph. It not only contains cycles of every possible length but also possesses another fascinating property. A bipancyclic graph has two vertices, known as endpoints, such that every other vertex lies on at least one cycle passing through both endpoints. In simpler terms, imagine a graph with two focal points and a network of cycles connecting those points, ensuring that every other vertex is included in at least one cycle between the two endpoints.

The Intricate Beauty of Pancyclic Graphs

Pancyclic graphs hold immense beauty in their intricate structures. These captivating mathematical entities offer a plethora of possibilities and provide valuable insights into the underlying patterns and connectivity of various systems. They represent a powerful tool for understanding complex networks, ranging from biological systems to social networks and even transportation networks.

One remarkable characteristic of pancyclic graphs is their potential application in designing efficient transportation systems. By analyzing the connectivity patterns within the graph, researchers can unearth optimal routes for transportation, minimizing congestion and reducing travel time for individuals. This can lead to significant improvements in transportation infrastructure and overall efficiency in urban planning.

Moreover, pancyclic graphs have proven to be indispensable in the field of biology. They provide a valuable framework for analyzing biological networks, such as protein-protein interaction networks and gene regulatory networks. By understanding the cyclical patterns within these networks, researchers can gain insight into crucial biological processes and uncover potential targets for drug discovery and therapy development.

In the world of social networks, pancyclic graphs play a crucial role in deciphering the dynamics of relationships and interactions between individuals. By mapping the connections within a social network onto a pancyclic graph, researchers can identify influential individuals, discover communities, and study the diffusion of information. This knowledge can be leveraged by businesses for targeted marketing strategies or policy-makers to promote positive societal changes.

Discovering the Marvels of Bipancyclic Graphs

As we delve further into the realm of graph theory, we encounter the mesmerizing bipancyclic graphs. These mysterious entities possess unique properties that set them apart from their pancyclic counterparts.

Bipancyclic graphs offer a valuable insight into the mutual accessibility of different vertices within a graph. By studying the connectivity patterns between the endpoints and other vertices, researchers can gain a deeper understanding of the overall structure and interconnectivity of various networks.

One exciting application of bipancyclic graphs lies in software engineering. These graphs help in analyzing software programs, enabling developers to identify potential vulnerabilities and loopholes within the code. By understanding the cyclical paths connecting different portions of the program, developers can strengthen security measures and ensure robustness in software frameworks.

Bipancyclic graphs also find application in network analysis and communication systems design. By studying the connectivity patterns between endpoints and other vertices, researchers can optimize the transmission of information within a communication network, leading to more efficient data flow and reduced latency. This knowledge is particularly valuable in today's fast-paced digital world, where seamless communication plays a vital role in various domains.

Pancyclic and Bipancyclic Graphs: A Journey Beyond

As we conclude our expedition into the captivating world of Pancyclic and Bipancyclic Graphs, we understand the profound impact these mathematical entities have on countless fields of study. The beauty of graph theory lies not only in its elegance and simplicity but also in its ability to uncover hidden patterns and connections within complex systems.

So, the next time you encounter a graph, remember the vast possibilities it holds within. Explore the realm of Pancyclic and Bipancyclic Graphs, and you'll embark on a journey to unravel new insights and embark on exciting discoveries.

Are you ready to delve into the fascinating world of graphs?

Pancyclic and Bipancyclic Graphs (SpringerBriefs in Mathematics)

by William Kercher(1st ed. 2016 Edition, Kindle Edition)

4.6 out of 5

Language	:	English
File size	:	3640 KB
Print length	:	120 pages
Screen Reader	:	Supported

FREE

This book is focused on pancyclic and bipancyclic graphs and is geared toward researchers and graduate students in graph theory. Readers should be familiar with the basic concepts of graph theory, the definitions of a graph and of a cycle. Pancyclic graphs contain cycles of all possible lengths from three up to the number of vertices in the graph. Bipartite graphs contain only cycles of even lengths, a bipancyclic graph is defined to be a bipartite graph with cycles of every even size from 4 vertices up to the number of vertices in the graph. Cutting edge research and fundamental results on pancyclic and bipartite graphs from a wide range of journal articles and conference proceedings are composed in this book to create a standalone presentation.

The following questions are highlighted through the book:

- What is the smallest possible number of edges in a pancyclic graph with v vertices?

- When do pancyclic graphs exist with exactly one cycle of every possible length?

- What is the smallest possible number of edges in a bipartite graph with v vertices?

- When do bipartite graphs exist with exactly one cycle of every possible length?